Tesis de Licenciatura en Ciencias de la Computación
“Sistema de optimización para el ruteo dinámico de
vehículos con ventanas de tiempo”
Eidelman, Adrián Pablo – L.U. 59/00
Valdez Lerena, Alejandro – L.U. 619/99
Directora: Dra. Irene Loiseau
Departamento de Computación
Facultad de Ciencias Exactas y Naturales
Universidad de Buenos Aires
Argentina
Septiembre 2007
Resumen
El problema de ruteo de vehículos con
ventanas de tiempo (VRPTW) consiste en la generación óptima de rutas de entrega
a partir de un conjunto estático de pedidos, considerando que cada pedido tiene
una locación y una banda horaria donde se debe realizar la entrega.
Este trabajo aborda el problema de VRPTW
con un conjunto de pedidos dinámico, es decir que durante la búsqueda de una
solución pueden ingresar nuevos pedidos, o extraerse conjuntos de pedidos del
sistema y el método de optimización debe tener en cuenta estos cambios en el
momento en que ocurren.
Este problema es de suma importancia en
empresas de logística, o que incluyan entre sus servicios la entrega de
productos a corto plazo y donde el conjunto de pedidos se modifique
frecuentemente. La utilización de herramientas informáticas para la resolución
de estos problemas representa una reducción importante en los costos asociados
al tamaño de una flota, el combustible requerido y el tiempo utilizado para la
entrega.
Para la resolución de problemas de este
tipo se diseñó un algoritmo basado en Búsqueda Tabú, aplicado sobre una
heurística de búsqueda local y se idearon distintas estrategias para mejorar la
calidad de las soluciones. Además se desarrolló un módulo que permite realizar
en forma batch el ingreso de pedidos y simular el avance del tiempo, así como
una interfaz gráfica para ver el estado de la simulación.
Abstract
The vehicle routing problem with time windows (VRPTW) consists of the
generation of optimal routes for delivery of a static set of orders,
considering that every order has a location and a time window where and when it
must be delivered.
This work takes on the VRPTW problem with a dynamic set of orders. This
means that during the search for a solution, new orders may arrive or sets of
orders can be removed from the system and the optimization method must take
this into account.
The DVRPTW is of utmost importance for logistic enterprises or for those
that include among their services the delivery of products in a short time
window and where the set of orders changes frequently. The use of computer
systems to solve this kind of problems represents an important reduction in the
costs associated with the fleet of vehicles, the fuel required and the delivery
delays.
To solve this kind of problems an algorithm based on Tabu Search applied
over a local search heuristic was designed and different strategies were devised
to improve the quality of the solutions. Besides, a module that allows the
adding of orders in batch and simulates the advance of time was developed as it
was also a graphic interface to see the state of the simulation.
Índice
Problemas de ruteo de vehículos
Elementos de la visión estática de nuestro problema
(VRPTW)
Objetivos de la visión estática del problema analizado
La versión dinámica del problema (DVRPTW)
Capítulo 4: Algoritmo propuesto
Aplicación del algoritmo de Búsqueda Tabú
Consideraciones generales de la implementación
Capítulo 6: Resultados obtenidos
Instancias propuestas por Solomon
Instancias generadas en forma aleatoria
Capítulo 1: Introducción
Introducción
Este trabajo aborda la problemática del
ruteo dinámico de vehículos con ventanas de tiempo. Este problema consiste en
la generación óptima de recorridos para realizar la entrega de pedidos a
domicilio, teniendo en cuenta que cada pedido debe ser entregado en una determinada
franja horaria y que además el conjunto de pedidos puede variar a medida que
transcurre el tiempo.
La variante estática de este problema, en
la que el conjunto de pedidos a optimizar se conoce desde el principio, suele
estar asociada a entregas programadas con anticipación. En esta situación el
tiempo disponible para obtener una buena solución no presenta una limitación
fuerte. En cambio, si el conjunto de pedidos varía frecuentemente, se presenta una
situación en la que generalmente las entregas son programadas con poca
anticipación y donde no puede haber demasiada demora entre el ingreso de un
pedido y su ubicación en un recorrido.
Entre los factores a considerar en la
generación de recorridos se encuentra la minimización del tamaño de la flota de
vehículos, acortando la distancia
recorrida y los tiempos de espera entre dos entregas de un mismo recorrido; así
como también el máximo aprovechamiento de la capacidad de transporte de cada
vehículo.
En
muchas empresas este tipo de tareas es realizada por una persona que organiza
la distribución de pedidos para cada recorrido. Sin embargo el tamaño del
conjunto de pedidos y la frecuencia de entrada de nuevos pedidos pueden llevar
a obtener recorridos en los que no se aproveche debidamente los recursos de la
flota de entrega, lo cual hace necesaria una herramienta como la planteada en
este trabajo.
El problema de ruteo de vehículos con
ventanas de tiempo pertenece a la clase NP-Hard. La variante abordada en este
trabajo donde el conjunto de pedidos varía a lo largo del tiempo es análoga a
encontrar la solución exacta a cada conjunto de pedidos antes de que se agregue
un nuevo pedido al conjunto, y por ende pertenece a la clase NP-Hard. Esto
significa que no se conoce ningún algoritmo polinomial que pueda encontrar una
solución exacta al problema.
Al ser este problema computacionalmente
intratable en la práctica para instancias medianas o grandes, deja como
alternativa la utilización de técnicas algorítmicas que puedan encontrar
soluciones aproximadas en tiempo polinomial. Ejemplo de estas técnicas son
Algoritmos Genéticos, Colonias de Hormigas, etc.
En este trabajo utilizamos como método para
aproximar soluciones una heurística de búsqueda local, que permite encontrar
soluciones razonablemente buenas (no necesariamente óptimas) en un tiempo
acotado, junto con una adaptación de una metaheurística de búsqueda Tabú para
evitar caer en óptimos locales y como mecanismo de exploración del espacio de
soluciones.
Capítulo
2: VRP y VRPTW
Problemas
de ruteo de vehículos
El planteo clásico del problema de ruteo de
vehículos (VRP) consiste en la
generación de un conjunto de rutas asignado a una flota de vehículos; estas
rutas recorren una serie de clientes donde se debe realizar la entrega de algún
producto. Generalmente el objetivo del problema es realizar la entrega en los
clientes minimizando el tamaño de la flota de vehículos y/o la distancia
recorrida por la misma. En su planteo clásico, los vehículos parten desde un depósito
central y deben volver allí al terminar su entrega.
Este tipo de problema aparece naturalmente
en la industria del transporte, distribución y logística, y su importancia
radica en que el costo de transporte suele ser un porcentaje significativo en
el valor asociado a un producto.
En aplicaciones de la vida real este
problema aparece en distintas variantes con diversos tipos de restricciones,
entre las más importantes se encuentran [TV02][VRPWEB]:
·
Cada vehículo tiene una capacidad de
almacenamiento finita (Capacitated VRP - CVRP)
·
El proveedor utiliza varios depósitos
para realizar la distribución (Multiple Depot VRP - MDVRP)
·
Los clientes pueden enviar productos
de vuelta al depósito. (VRP
with Pick-Up and Delivery - VRPPD)
·
Varios vehículos pueden satisfacer en
forma conjunta un pedido de un cliente (Split Delivery VRP - SDVRP)
·
Las entregas deben realizarse en
ciertos días (Periodic VRP - PVRP)
·
Cada cliente debe ser visitado dentro
de una determinada ventana de tiempo. (VRP with time windows - VRPTW)
Elementos
de la visión estática de nuestro problema (VRPTW)
Área de distribución
La distribución de productos se realiza dentro
de un área determinada. Una forma conveniente de representar el área es por
medio de una cuadrícula. Cada celda en la cuadrícula representa una zona dentro
del área de distribución, a los efectos del problema que un vehículo llegue a
una celda es lo mismo que si hubiera llegado al domicilio del cliente. Esta
abstracción nos independiza de los detalles de un recorrido detallado a través
de las calles de una ciudad y permite focalizarnos en el problema a resolver.
Pedidos
Cada pedido a entregar está asociado a un
solo cliente, tiene un tamaño fijo y una banda horaria (también llamada ventana
de tiempo) donde el cliente espera la entrega. El conjunto de pedidos es
conocido al comenzar el problema y no varía hasta encontrar una solución al mismo.
Recorridos o rutas
Llamamos recorrido o ruta a una secuencia
de pedidos de entrega, que parte y termina en el depósito central. Cada ruta es
asignada a un vehículo y se asume que el vehículo tendrá éxito en la entrega de
los productos. Para medir la distancia recorrida en cada ruta se utiliza como
métrica la distancia euclidiana entre cada par de puntos que componen el
recorrido.
Flota
Consideramos que la flota de distribución
está formada por un conjunto homogéneo de vehículos, donde todos tienen la
misma capacidad (finita) de almacenamiento
y pueden tener asignada una sola ruta.
Factibilidad de las rutas
Diremos que una ruta es factible cuando se
puede realizar el recorrido completo cumpliendo las ventanas de tiempo de todos
los pedidos y sin exceder la capacidad del vehículo.
Solución
Teniendo en cuenta las consideraciones
anteriores llamaremos solución a un conjunto de rutas factibles en las que
estén incluidos todos los pedidos que forman parte del problema. La hora en la
que cada vehículo debe partir del depósito también forma parte de la solución y
puede ser fácilmente calculada a partir del conjunto de rutas.
Objetivos
de la visión estática del problema analizado
El objetivo del problema de ruteo de
vehículos estático con capacidad limitada y ventanas de tiempo consiste en
encontrar un conjunto de rutas que optimice algunos o todos los siguientes
aspectos de la solución:
·
Minimice la cantidad de viajes necesarios
para realizar las entregas.
·
Minimice el tiempo de espera entre
entregas consecutivas de una ruta.
·
Minimice la distancia recorrida.
·
Minimice el tiempo de entrega a cada
cliente.
·
Maximice la capacidad utilizada en
cada vehículo para una ruta dada.
La optimización de estas variables implica
una reducción significativa en los costos asociados al transporte de productos.
La minimización de la cantidad de viajes permite reducir el tamaño de la flota
lo cual es importante si se tiene en cuenta el costo asociado a un vehículo y
su mantenimiento. Optimizar el tiempo de espera entre entregas permite realizar
mayor cantidad de entregas en un mismo lapso de tiempo y reduce el costo de
entrega por producto. La disminución de la distancia recorrida permite un
ahorro en los costos de combustible y desgaste de los vehículos, además la
distancia recorrida está asociada al tiempo que demora la entrega por lo que
minimizar esta variable también implica una mayor cantidad de productos
entregados por unidad de tiempo. Minimizar el tiempo de entrega a los clientes
no trae un beneficio inmediato en los costos, pero mejora la calidad del
servicio que se está brindando. Por último maximizar la utilización de cada
vehículo ayuda a disminuir la cantidad de vehículos necesarios para realizar el
reparto y disminuye el costo de entrega por cada producto.
La
versión dinámica del problema (DVRPTW)
En la versión dinámica del problema, el
conjunto de pedidos a distribuir varía a medida que transcurre el tiempo. El mismo
aumenta cada vez que se agrega un pedido nuevo y disminuye cada vez que parte
un vehículo a realizar un recorrido eliminándose los pedidos que participan en
esa ruta.
Las variables a optimizar son las mismas
que en la versión estática, siendo necesario obtener una solución óptima luego
de cada variación del conjunto de pedidos. Esta característica aumenta de
manera notoria la dificultad del problema respecto a la versión estática debido
a que la constante variación en el conjunto de pedidos produce que una
asignación óptima de rutas deje de serlo luego de una modificación en el mismo.
Por otro lado, en muchos tipos de
industrias se dispone de un tiempo relativamente corto entre el ingreso de un
pedido que debe ser entregado y la hora más tardía a la que dicho producto puede
ser recibido. Esto plantea un desafío importante sobre el aprovechamiento del
tiempo de cómputo para obtener una solución factible y razonablemente buena en
lapsos de tiempo potencialmente muy cortos.
El
problema a resolver
A continuación detallaremos las
características particulares del problema de ruteo dinámico de vehículos que
nosotros decidimos resolver en base a las necesidades reales de un negocio de
delivery.
Se supone que la cantidad de vehículos es
ilimitada, esto permite asegurar que siempre es posible encontrar una solución
para cualquier conjunto válido de pedidos porque trivialmente se puede asignar
un pedido a cada vehículo. De esta forma se garantiza que puedan ingresar pedidos
con muy poca anticipación al momento más tardío en que deben partir del depósito
para cumplir con su ventana de tiempo. Por otro lado no presenta una desviación
importante de la realidad, ya que la empresa de logística puede alquilar
temporalmente vehículos adicionales a algún proveedor de servicios (en el caso
particular que analizamos, por tratarse de un delivery de pedidos mediante
motos, contamos con empresas que proveen rápidamente nuevos vehículos en caso
de ser necesarios).
Se agrega la restricción de que un producto
no puede estar en tránsito más de un determinado tiempo. Algunos productos se
deterioran a partir de la salida del depósito, por ejemplo productos
alimenticios para consumo inmediato, luego es necesario tener en cuenta esta
restricción para lograr entregar el producto en su calidad óptima.
El tamaño de los pedidos puede ser variable
pero deben caber en un solo vehículo. Además una vez que se realiza el pedido
de entrega no es posible cancelarlo ni modificar su ventana de tiempo.
Se supone que todos los vehículos se
desplazan a la misma velocidad, esta simplificación es necesaria si se tienen
en cuenta los distintos factores que afectan el tiempo empleado en efectuar el
recorrido como ser las características del tránsito según la zona, las
condiciones climáticas, posibles desperfectos mecánicos y otras eventualidades
que afectan la velocidad promedio de los vehículos. En una aplicación real se
debería encontrar un estimador de la velocidad que lleva el promedio de los
vehículos de la flota en base a datos estadísticos.
Asumimos que la ventana de tiempo de cada
pedido permite ser cumplida al momento que ingresa el mismo al sistema, esto implica
que el tiempo de viaje de un vehículo que parta desde el centro de distribución
directamente al cliente no puede ser mayor al tiempo que resta para el fin de
la ventana de entrega del pedido. De
este modo se garantiza que sea posible encontrar una solución factible para
cualquier conjunto de pedidos que exista en el sistema.
Los objetivos planteados para la
optimización son los mismos que los que fueron planteados para la versión estática
del problema.
Antecedentes del problema
A diferencia de lo que uno podría suponer
en primera instancia, el DVRPTW no es un problema que haya sido tratado tan
extensamente en la bibliografía como las versiones estáticas. Sin embargo,
pudimos encontrar algunos papers que trataban el tema aunque con algunas
variantes respecto del planteado por nosotros. Por ejemplo, [BH04] plantea un
escenario donde parte de los pedidos son conocidos y fijos de antemano y a
medida que se van satisfaciendo van entrando nuevos pedidos. Utiliza para la
resolución del problema el planteamiento de varias soluciones candidatas y una
función de consenso para determinar cual es la solución principal. [TV03]
presenta la idea de búsqueda Tabú granular (la búsqueda Tabú es definida en el
siguiente capítulo). Esta consiste en restringir el vecindario a analizar lo
más posible pero manteniendo dentro del mismo aquellos vecinos que parecen proveer
buenas soluciones. En base a esta idea de restricción fue que desarrollamos uno
de nuestros aportes al análisis del problema y que consiste en restringir el
análisis de posibles soluciones en base
al radio de acción (el cual se define en el capítulo 4). A pesar de haber
encontrado estos y algunos papers más sobre el tema, no nos fue posible conseguir
instancias y sus resultados para poder usarlos como punto de comparación con la
solución implementada.
Capítulo
3: Búsqueda Tabú
Búsqueda
Tabú
Una forma frecuente de abordar los
problemas que son NP-Hard [GJ79] es la utilización de técnicas heurísticas (por
ej. de búsqueda local), que en general no obtienen soluciones óptimas, pero sí
lo suficientemente buenas utilizando un escaso tiempo de cómputo. En la mayoría
de los casos la cantidad de operaciones de los algoritmos hasta ahora conocidos
que encuentran una solución exacta a problemas de este tipo son exponenciales
respecto al tamaño de la entrada, haciendo prohibitiva su utilización para
conjuntos de datos de tamaño considerable.
A continuación se realiza una breve
exposición de los conceptos básicos relacionados a las técnicas de búsqueda
local y a las metaheurísticas.
Métodos
de búsqueda local
En general, los problemas de optimización
combinatoria pueden verse como el de encontrar una solución dentro del espacio
de soluciones factibles, que minimice o maximice una función cuyo dominio son
los aspectos a optimizar del problema y su imagen un número real. Se llama función objetivo a la función cuyo mínimo o máximo
se está buscando. Luego, una solución óptima al problema será aquella cuyo
valor de función objetivo sea mínimo o máximo.
Dada una solución S del problema a
optimizar, se llama solución vecina a
aquella que resulta de la aplicación de algún cambio pequeño en S. Esto permite
definir una vecindad o conjunto de
vecinos que son las soluciones resultantes de aplicar algún cambio
pequeño (también llamado movimiento) en la
solución S.
Las heurísticas de búsqueda local tienen
por objetivo minimizar el valor de la función objetivo a partir de una solución
inicial S, explorando los valores de esa función para las soluciones
pertenecientes a la vecindad de S y preservando como nueva mejor solución
aquella que obtuvo el menor valor de la función objetivo. Una aplicación
sucesiva de esta técnica lleva eventualmente a encontrar una solución que
minimice la función objetivo dentro de su vecindario, situación que suele
utilizarse como criterio de parada para la búsqueda local.
A las soluciones obtenidas de este modo se
las suele llamar mínimos locales, en el
sentido de que minimizan la función objetivo en la vecindad que definen, pero
no hay garantía de que esa solución sea también un mínimo
global para la función objetivo. Esta es la principal debilidad de este
tipo de algoritmos puesto que el mínimo local encontrado podría estar muy
alejado del mínimo global.
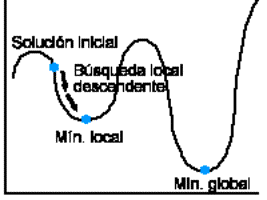
Fig. 01. Detalle de funcionamiento de búsqueda local
en relación a mínimos locales y globales
Para evitar estancarse en un mínimo local,
es necesario permitir la aplicación de movimientos
de no mejora que, empeorando la calidad de la solución, la alejen del
mínimo local encontrado y permitan encontrar otro nuevo y mejor mínimo local.
Al permitir la utilización de movimientos de no mejora es posible la aparición
de ciclos en las soluciones que se evalúan, situación que será analizada en
apartados posteriores.

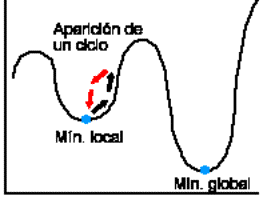
Fig. 02. Movimientos de no mejora para salir de
mínimos locales y Fig.03. posible aparición de ciclos
Metaheurísticas
Las metaheurísticas son técnicas para la
búsqueda de soluciones en dominios en los que esta tarea es compleja. En
general utilizan los resultados de una heurística, por ejemplo de una búsqueda
local, para llevar a cabo su tarea.
Existe una gran variedad de técnicas
metaheurísticas, distintas aproximaciones utilizan distintos métodos como
principios de funcionamiento, entre ellas se pueden citar GRASP, Simulated Annealing, Ant Colony, Tabú
Search, Algoritmos Genéticos, etc.
Entre las técnicas utilizadas por las
metaheurísticas se encuentran la utilización de algún componente aleatorio en
la exploración del espacio de soluciones, el almacenamiento de un conjunto de
soluciones candidatas que por alguna característica parecen promisorias y deben
ser posteriormente analizadas, la aplicación del concepto de intensificación
(explorar con más detalle cierto conjunto de soluciones) y diversificación
(explorar soluciones distantes para alejarse de mínimos locales) y la
utilización de técnicas probabilísticas.
Conceptos
sobre Búsqueda Tabú
Introducción
La Búsqueda Tabú [G89, GL93] es una
metaheurística utilizada frecuentemente en problemas de optimización combinatoria.
Se basa en un procedimiento iterativo de exploración guiada en el espacio de
soluciones del problema a tratar. La forma actual en que se utiliza el método
fue presentada en 1986 por Glover [G86]. Por el momento no se conoce una
demostración formal sobre su buen comportamiento. Sin embargo se lo utiliza
exitosamente en numerosas aplicaciones teóricas como coloreo de grafos,
viajante de comercio, clique máximo y otras. La técnica ha sido ampliamente
aceptada debido a la aplicación exitosa en problemas prácticos como diseño de
circuitos de alta integración (VLSI), scheduling de tareas, diseño de redes
tolerante a fallos, entre muchos otros.
El algoritmo basa su funcionamiento en los
conceptos de exploración inteligente y memoria adaptativa. Ambas ideas sugieren la noción
de aprendizaje, en el sentido de que se utilizan los datos recolectados al
realizar la tarea (memoria) para influir en la toma de decisiones (exploración
inteligente) que se espera lleven a buenos resultados. La utilización de una
memoria como parte del algoritmo lo diferencia de otras técnicas como los
algoritmos genéticos que no hacen uso de esta; por otro lado la característica
de adaptativo lo distingue de métodos como Branch & Bound donde se posee
una memoria rígida. La exploración inteligente,
se basa en la suposición de que existe más información en la toma de una mala
decisión estratégica (ya que esa decisión sirve como referencia para futuras
decisiones), que en una buena decisión tomada al azar que no provee información
para decisiones futuras.
En esencia el algoritmo de Búsqueda Tabú
explora el espacio de soluciones realizando la aplicación sucesiva de movimientos a partir de una solución inicial. Como
se explicó anteriormente al hablar de la búsqueda local un movimiento es alguna
variación pequeña en la estructura de una solución que produce una nueva
solución distinta. Se llama vecindad o conjunto de vecinos a las soluciones que pueden
obtenerse aplicando un determinado tipo de cambio a una solución dada. En
general el algoritmo se mueve hacia la mejor
solución que pueda hallar en la vecindad de la solución actual que esté
considerando. Sin embargo, a veces puede realizar movimientos en los que la
solución obtenida es peor en busca del mínimo global. Esta sucesión de
movimientos podría producir la aparición de ciclos en las soluciones a analizar
(visitar alternadamente las mismas soluciones), para evitar esta situación el
algoritmo mantiene un conjunto de movimientos prohibidos (lista tabú) que no deben realizarse por una
determinada cantidad de iteraciones (tabú tenure).
La lista tabú puede contener distintos tipos
de información según el problema que se esté analizando y el efecto que se
quiera lograr en la exploración del espacio de soluciones. Se llama memoria explícita a aquella en la que se almacena
el contenido de una solución entera; por otro lado se llama memoria atributiva cuando se almacenan algunas
características de las soluciones visitadas.
En la Búsqueda Tabú también puede hacerse
una distinción entre la utilización de una memoria a corto o largo plazo. Un
ejemplo de memoria a corto plazo es almacenar los movimientos reversos a los
realizados recientemente a fin de evitar volver a visitar una solución ya
analizada. Por otro lado la memoria a largo plazo suele estar relacionada con
la frecuencia de ocurrencia de determinados atributos en las soluciones
visitadas y se la puede utilizar para privilegiar o prohibir movimientos que
lleven a soluciones con atributos que fueron vistos frecuentemente en iteraciones
pasadas.
Para evitar el estancamiento en soluciones
localmente óptimas, el algoritmo permite la realización de movimientos que
empeoren la calidad de la solución a fin de lograr encontrar un camino por el espacio de soluciones que permita
llegar a una solución de mejor calidad. También se utiliza el llamado criterio de aspiración que permite realizar
movimientos (prohibidos) que se encuentren en la lista tabú cuando estos
permitan alcanzar soluciones de mejor calidad que las vistas hasta el momento.
El criterio de parada para este tipo de
algoritmo suele estar dado por la realización de una determinada cantidad de
iteraciones en las que no se encuentre una mejora de la solución. Otros
criterios pueden ser la utilización de una cota de tiempo o un valor de umbral
en el que se considere que la solución obtenida es suficientemente buena para
la aplicación en cuestión.
Algoritmo de Búsqueda Tabú
1)
Dada una solución inicial i; i*=i;
k=0.
2)
k=k+1; Generar el conjunto de vecinos
V* de V(i,k), tal que cumpla las condiciones impuestas por la lista tabú o
cumpla el criterio de aspiración.
3)
Elegir el mejor j e V* con respecto a f(j) y hacer
i=j.
4)
Si f(j) < f(i*), hacer i*=j.
5)
Actualizar la lista tabú.
6)
Si no se cumple el criterio de parada
ir a 2)
El algoritmo de la búsqueda Tabú (ver
recuadro superior) parte de una solución inicial i, que pudo haber sido
obtenida por algún procedimiento aleatorio, greedy
u otro, desde donde se comienza a recorrer el espacio de soluciones. La función
V(Solución i, Número de iteración k) genera el conjunto de soluciones vecinas a
S descartando aquellas que no se puedan utilizar por restricciones en la lista
tabú, pero incluyendo aquellas que debido al criterio de aspiración puedan
ignorar la prohibición de la misma. Entre todas las soluciones de la vecindad
de S se selecciona aquella que minimice el valor de la función objetivo
f(Solución i), en caso de que la mejor solución de la vecindad (j) supere en
calidad a la mejor obtenida hasta ese momento (i*), se toma a j como la nueva
mejor solución.
Luego se realiza la actualización de la
lista tabú que, como esquema básico y a fines de evitar ciclos en las
soluciones que se analizan, puede consistir en almacenar el movimiento inverso
al realizado al pasar de la solución i* a la solución j. Dentro de la
actualización a la lista tabú también se incluye la eliminación de movimientos
viejos de acuerdo al tenure que se haya
definido para la lista, así como la actualización de la memoria de largo plazo
(si la hubiera) donde podría llevarse una cuenta de la cantidad de veces que se
visitaron distintas soluciones.
Por último se verifica el criterio de
parada y en caso de no cumplirse se repite nuevamente el procedimiento.
Cabe destacar que la elección de la función
V() debe realizarse con sumo cuidado. Una mala elección podría ser tomar un
vecindario que tuviera un tamaño exponencial respecto de los datos de entrada,
en esa situación el algoritmo tendría una convergencia mucho más lenta. Por
otro lado, en circunstancias en las que la vecindad sea más grande que lo
deseado puede tomarse un subconjunto en forma aleatoria, reduciendo
arbitrariamente la cantidad de soluciones vecinas a analizar.
Estrategias de búsqueda
Existen diversas técnicas que permiten
modificar el comportamiento del algoritmo al momento de explorar el espacio de
soluciones, permitiendo concentrarse en determinadas zonas (intensificación),
explorar soluciones distantes (diversificación) y almacenar soluciones
candidatas que resultaron interesantes por alguna característica distintiva (soluciones
elite).
Intensificación
La intensificación se refiere a explorar en
mayor detalle una determinada zona del espacio de soluciones, con la expectativa
de encontrar en ese conjunto una solución mejor a las conocidas. La
intensificación puede estar motivada por alguna característica sobresaliente de
una solución o conjunto de soluciones, sea en su calidad o basada en algún
conjunto de atributos que estén asociados a buenas soluciones.
Existen diversas maneras de implementar
esta técnica, la más simple consiste en disminuir el tamaño de la lista tabú,
de modo que se permitan más movimientos de retroceso que, a riesgo de generar la
ocurrencia de ciclos, permitan una exploración más detallada de una determinada
zona. Otra alternativa consiste en modificar el criterio de selección de
movimientos a fin de privilegiar aquellos que estén asociados a atributos que
aparecen frecuentemente en soluciones buenas.
Diversificación
Conceptualmente contraria a la estrategia
de intensificación, la diversificación pretende analizar regiones lejanas a la
actual en el espacio de búsqueda, con la intención de escapar a óptimos locales
y evitar que queden zonas sin visitar en el espacio de soluciones.
Una forma simple de implementar este
comportamiento consiste en aumentar el tamaño de la lista tabú, con el fin de
que al aumentar la cantidad de soluciones prohibidas en la zona que se está
explorando se fuerce al algoritmo a orientar la búsqueda en nuevas zonas que se
alejen de la actual.
También puede realizarse una diversificación
modificando las reglas de selección de movimientos, a fin de que se privilegie
la utilización de atributos que no fueron empleados frecuentemente en las
soluciones analizadas hasta el momento.
Otra manera trivial de realizar una
diversificación es detener el algoritmo y comenzar una nueva búsqueda a partir
de una nueva solución inicial. Esta nueva solución podría generarse utilizando
una combinación de los atributos comunes que generalmente forman parte de las
soluciones buenas junto a un componente aleatorio, o bien en forma
completamente aleatoria. El empleo frecuente de diversificaciones a partir de
soluciones aleatorias proporciona una buena posibilidad de cubrir una región
extensa del espacio de soluciones.
Tamaño dinámico en la lista tabú
La variación dinámica del tamaño de la
lista tabú, permitiendo el almacenamiento de una cantidad mayor o menor de
movimientos prohibidos, permite combinar en forma conveniente las dos
estrategias que acaban de exponerse.
Un aumento en el tamaño de la lista tabú puede
verse como una diversificación, mientras que una disminución puede considerarse
como una intensificación. La variación en el tamaño de la lista podría estar
motivada en base a la frecuencia de aparición de determinados atributos en las
soluciones que se visitaron recientemente, o bien en un componente aleatorio.
La combinación de intensificación y diversificación permite una exploración
amplia y detallada del espacio de soluciones que permite aumentar las posibilidades
de encontrar mejores óptimos locales.
Soluciones Elite
Se llaman soluciones elite a aquellas
soluciones buenas que fueron exploradas durante el proceso de búsqueda y que
por algún motivo se destacan del resto, ya sea por alguna característica en sus
atributos o por tener valores de la función objetivo cercanos al mejor valor
conocido. En general estas soluciones se las almacena en una lista para ser
exploradas mediante un proceso de intensificación en momentos posteriores de la
búsqueda.
Capítulo
4: Algoritmo propuesto
Algoritmo
propuesto
Solución inicial
En el capítulo anterior se mencionó que la Búsqueda
Tabú se realizaba a partir de una solución inicial. Dependiendo de la
naturaleza del problema a tratar esa solución inicial puede tener distinto
nivel de influencia en la calidad de la solución obtenida a través del
algoritmo de Búsqueda Tabú.
En la variante dinámica del problema de
ruteo el conjunto inicial de pedidos a entregar es vacío y crece con el
transcurso del tiempo a medida que se agregan nuevos pedidos a distribuir. Luego,
la primera solución considerada por la Búsqueda Tabú es trivialmente la
solución vacía.
Heurística de inserción
Al momento de ingresar un nuevo pedido al
sistema se plantea la dificultad de cómo incorporar ese pedido al conjunto de
rutas existentes, tratando en lo posible de no deteriorar la calidad de la
solución y teniendo en cuenta una serie de criterios deseables respecto a la inserción
de un nuevo elemento dentro de una solución. A continuación presentamos las características
que consideramos deseables sobre el proceso de inserción:
1) Que sea rápido. Es importante que el nuevo pedido forme parte de la
solución tan pronto como sea posible. Esto se debe a que un retardo en su
incorporación podría implicar que no se pudiera cumplir con su ventana de
tiempo si esta estuviera pronta a vencer. Además permite que el sistema admita
el ingreso de una gran cantidad de pedidos en un corto lapso de tiempo.
2) Que preferentemente la solución resultante de la inserción sea
factible. Al tratarse de un sistema on-line, en el cual los pedidos pueden
ingresar en cualquier momento, es preferible mantener en forma permanente la
factibilidad de la solución. De este modo se evita la necesidad de realizar
cambios para hacer factible la nueva solución, y permite aprovechar ese tiempo
para que la metaheurística explore el nuevo espacio de soluciones donde
participa el nuevo pedido.
3) Que minimice el costo de la solución. Está claro que si el objetivo
final del sistema es encontrar la solución de menor costo, es deseable que al
agregar un nuevo pedido se obtenga una nueva solución que incluya el nuevo
pedido y que tenga el menor costo posible.
Teniendo en cuenta las distintas características
planteadas, consideramos los siguientes criterios para la inserción de un nuevo
pedido:
·
Hacer una búsqueda exhaustiva para
encontrar la mejor posición en donde insertar el pedido dentro de las rutas
existentes.
·
Insertarlo en forma golosa (recorriendo
cada posición de cada ruta) dentro de los recorridos ya existentes, y en caso
de no poder agregarlo en ningún recorrido ponerlo en una ruta nueva.
·
Poner el pedido en una ruta nueva.
La primera alternativa parece más adecuada
dado que el principal objetivo del sistema es minimizar el costo de la solución
y la búsqueda de la mejor posición para insertar un pedido tiene orden lineal
respecto a la cantidad de pedidos en el sistema.
La segunda alternativa no presenta una
mejora respecto de la primera pero es superior a la tercera en el sentido de
que intuitivamente se prefiere una solución que utilice una menor cantidad de
rutas.
Por último, agregar el pedido en una ruta
nueva tiene como ventaja que la inserción es O(1) sin importar el tamaño de la
solución actual ni la cantidad de rutas o pedidos que tenga. Por otra parte
permite que el algoritmo Tabú explore las distintas formas de incorporar el
nuevo pedido al resto de la solución, de modo de permitirle aprender de esa información.
Inicialmente se optó por la primera
alternativa, pero la experiencia empírica nos llevó a obtener mejores
resultados adoptando la tercera. Esto se debe a la característica on-line del
problema tratado, en el sentido de que hay pedidos que ingresan con muy poco
tiempo de anticipación a su vencimiento siendo mas útil en esos casos permitir
que el tiempo de cómputo se utilice en el mejoramiento de la solución más que
en una inserción inicial de mejor calidad. Si el poco tiempo disponible se
invierte en encontrar la mejor posición de inserción del último pedido, se
pierde la oportunidad de analizar con mayor profundidad las rutas próximas a vencerse.
Heurísticas
de mejora
A continuación presentamos las distintas
estrategias que utilizamos para a partir de una solución lograr encontrar otra
nueva con un costo menor. Esto dará pie para presentar posteriormente la
estructura del vecindario para el algoritmo de Búsqueda Tabú.
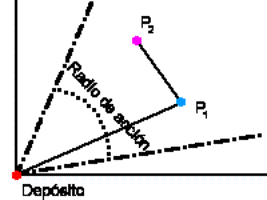
Radio de acción
Una de las ideas introducidas por nosotros
en el análisis del problema y que no vimos en ningún otro material al que
tuvimos acceso es el concepto de Radio de Acción. El radio de acción de una
ruta es la máxima amplitud angular que puede tener la misma tomando como origen
de coordenadas al centro de distribución. Los siguientes gráficos ilustran este
concepto:
|
|
|
|
Fig. 04. Radio de acción para una ruta
simple |
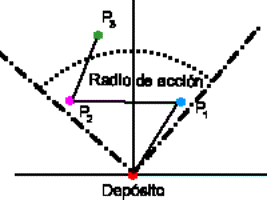
Fig. 05. Radio de acción con 3 pedidos
donde se ve que el mismo se mantiene centrado respecto de los pedidos más
alejados angularmente. |
Un valor demasiado grande del radio de
acción tenderá a producir rutas con recorridos extensos en distancia que en
general atentan contra la calidad de la solución. Por otro lado, un valor demasiado
chico tenderá a producir rutas con
pedidos más cercanos entre si, pero a la vez producirá un mayor número de rutas
lo cual también atenta contra la calidad de la solución.
El Radio de acción, permite restringir el
análisis de la búsqueda Tabú a un número mucho menor de movimientos (esto se ve
más adelante en análisis del vecindario)
ya que solo se analiza un posible movimiento si las rutas de origen y
destino poseen una intersección en su radio de acción.
La selección de este valor es global para
todas las rutas y se pretende que se adopten valores basados en la experiencia.
El método para calcular el radio de acción
de una ruta es bastante sencillo. Se toman los dos pedidos cuyo ángulo respecto
del depósito posee mayor diferencia. Luego al ángulo del radio de acción (que
está fijo por ser un parámetro de la simulación) se le resta la diferencia
entre los ángulos de los dos pedidos y se le suma a cada uno esa diferencia
dividida por dos. De esta manera el radio de acción siempre queda centrado
respecto de los dos pedidos con mayor diferencia angular.
Intercambios Or-Opt
Los intercambios Or-Opt [O76] son un
mecanismo de mejora ampliamente utilizado en distintas variantes del problema
de ruteo de vehículos, variantes de TSP, y otros problemas similares. El
mecanismo se aplica a un determinado par de rutas, una de ellas será la ruta
origen, y la otra la ruta destino, el intercambio consiste en mover una
secuencia de entre 1 y 3 vértices consecutivos desde la ruta de origen a algún
lugar de la ruta de destino. A continuación se presentan unos gráficos para
clarificar el concepto:
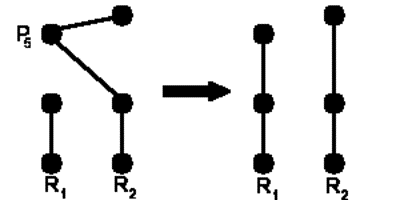
Fig. 06. Intercambio Or-Opt del pedido 5 de la ruta
2 al final de la ruta 1
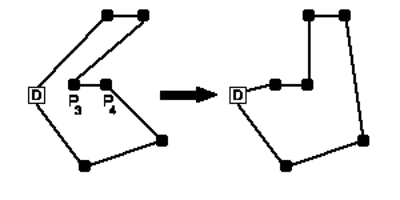
Fig. 07. Intercambio Or-Opt de los pedidos 3
y 4 hacia el inicio de la ruta
La metaheurística utiliza esta herramienta
como heurística de mejora. Una vez seleccionadas las rutas de origen y destino,
el algoritmo selecciona de la ruta de origen todas las subsecuencias de 1, 2 y
3 vértices consecutivos e intenta insertarlos en todas las posibles posiciones
de la ruta de destino. Este procedimiento tiene O(n2) con n la
cantidad de pedidos de la ruta más larga.
En caso de existir, se obtiene como
resultado de este proceso un movimiento de pedidos de una ruta a otra, manteniendo
la factibilidad de la solución.
Selección de rutas a optimizar
Una vez seleccionado el mecanismo de
intercambio de pedidos entre rutas, el siguiente paso consiste en encontrar una
manera de elegir las rutas que intervendrán en los intercambios con la
intención de que un determinado criterio de selección permita obtener un menor número
de rutas, con mayor cantidad de pedidos por rutas y una solución de costo
menor. Consideramos los siguientes criterios de selección para las rutas de
origen y destino:
1) Tomar como origen las rutas con menor cantidad de pedidos, y como
destino las rutas con mayor cantidad de pedidos.
2) Tomar como origen y como destino las rutas con mayor cantidad de
pedidos.
3) Tomar como origen y como destino las rutas con menor cantidad de pedidos.
4) Tomar las rutas de origen y destino en forma aleatoria.
5) Tomar las rutas que tienen hora de vencimiento más próxima a la hora
actual.
El primer criterio pretende que al mover
pedidos de rutas con pocos pedidos hacia rutas con muchos pedidos, eventualmente
las rutas con pocos pedidos queden vacías y desaparezcan del sistema. Este mecanismo
asegura que los pedidos recién ingresados (que se agregan en una ruta aparte)
se incorporen al conjunto de rutas largas, lo cual minimiza la importancia de
que el mecanismo de inserción de nuevos pedidos utilice una ruta extra por cada
pedido ingresado.
En el segundo criterio se espera que rutas
de similar longitud compartan características similares, y esto facilite
encontrar movimientos viables que aumenten la cantidad de pedidos que entrega
un vehículo. Este mecanismo puede producir que los pedidos recién ingresados no
sean tratados y genere un número importante de rutas y una solución muy alejada
de la óptima.
En el tercer caso se supone que las rutas
largas son lo suficientemente buenas como para ser aceptadas y se vuelve a
plantear la idea de privilegiar la integración de los pedidos recién ingresados
y las rutas con menor cantidad de pedidos. En este caso se espera obtener un
conjunto de rutas con una cantidad similar de pedidos en cada una. Esto se debe
a que no se intensifica el tratamiento de ningún conjunto específico de rutas.
El criterio aleatorio pretende evitar
posibles casos de inanición que la rigidez del resto de los criterios podría
producir. Sin embargo no realiza ninguna tarea específica para incorporar los
pedidos recién ingresados ni privilegiar el tratamiento de ningún tipo de ruta.
Finalmente, el quinto criterio plantea la
importancia de la característica on-line de este trabajo, y presta más importancia
a las rutas que están por partir del depósito debido al vencimiento en el
horario de entrega de alguno de sus pedidos. Este mecanismo supone que es más
importante tratar de mejorar las rutas que están prontas a vencerse en vistas
de que pronto dejarán de formar parte del sistema y no podrán ser optimizadas
por mucho más tiempo.
En nuestra experiencia encontramos que los
distintos criterios sufren de distintas limitaciones, no siendo adecuado
ninguno de ellos por sí solo. En la mayoría de los casos las soluciones
encontradas al implementarlos individualmente presentaban valores muy alejados
del mejor resultado conocido, mayormente debido a que su rigidez producía la
generación de un subconjunto de rutas que era tratado reiteradamente sin
producir ninguna mejora, mientras que otros subconjuntos de rutas no eran
seleccionados por la heurística para su análisis. Por lo tanto, decidimos
empezar a probar combinaciones de los mismos, tratando de que la mezcla lograse
compensar las deficiencias y aprovechar las buenas cualidades de cada uno.
Estas combinaciones las fuimos comprobando con distintos conjuntos de datos
pequeños para poder realizar comprobaciones manuales de los resultados
obtenidos.
Esto nos llevó a plantear el siguiente
criterio de selección de rutas que experimentalmente obtuvo el mejor resultado
en la generación de soluciones:
1) Intentar unir los pedidos pertenecientes a rutas de longitud uno
(generalmente, los pedidos recién ingresados) a las rutas de longitud mayor.
2) Seleccionar aleatoriamente un conjunto de rutas X de tamaño t que
serán tratadas como rutas de origen.
3) Seleccionar aleatoriamente un conjunto de rutas Y de tamaño t que
serán tratadas como rutas de destino (X e Y pueden tener elementos en común).
Cabe aclarar que en ninguno de estos pasos se utiliza el Radio de acción, ya que en este momento no queremos restringir el análisis a rutas con una dirección en particular sino poder analizar todas las orientaciones.
Nivel de ocupación de la ruta
Es parte del problema la suposición de que
todos los vehículos tienen una capacidad de transporte finita, luego un aspecto
a considerar durante la selección de rutas para la aplicación de intercambios
Or-Opt es qué porcentaje del espacio del vehículo se considera aceptable o,
visto de otro modo cuánto espacio se puede desperdiciar en cada vehículo sin
que esto deteriore demasiado la calidad de la solución.
El objetivo ideal sería lograr la máxima
ocupación posible en cada vehículo. Intuitivamente esto tiende a disminuir la
cantidad de rutas empleadas para realizar la distribución de todos los pedidos
que ingresan al sistema. Sin embargo observamos que priorizar demasiado este
objetivo implicaba la selección frecuente de un conjunto de rutas a las que se
intentaba mejorar sin éxito.
Por otra parte, la relajación de este
objetivo produce rutas en las que no se aprovecha eficientemente la capacidad
de cada vehículo, lo cual nos llevó a fijar un umbral donde se considera que el
vehículo asociado a una ruta está lo suficientemente completo y serán
privilegiadas en la selección de rutas a optimizar aquellas que tengan un nivel
de ocupación por debajo del umbral.
Esta decisión se ve reforzada al tener en
cuenta la característica on-line del sistema. El tiempo desde que un pedido
ingresa al sistema, hasta que llega el momento de que el vehículo que lo
transporta parta del depósito puede ser bastante corto. Por lo tanto es
necesario intentar tener la mayor cantidad de rutas con un nivel de ocupación
aceptable tan pronto como sea posible, evitando invertir tiempo en intensificar
la búsqueda para mejorar la calidad de algunas rutas.
Movimientos fallidos por ruta
Llamamos movimiento a cada intento de mover
un pedido o secuencia de pedidos desde una ruta de origen a una ruta de destino.
Un factor que creímos sería de utilidad fue la selección de rutas como destino
basado en la cantidad de veces que se logró mejorar esa ruta; o análogamente, basado
en la cantidad de intentos de realizar un movimiento que no tuvo éxito.
De este modo se pretendía llevar la cuenta
de la cantidad de movimientos fallidos por ruta, y luego privilegiar en la
selección de rutas de destino a aquellas con menor cantidad de intentos
fallidos. Contrario a lo esperado este criterio no mostró mejoras
significativas y se eliminó de la implementación.
Aplicación
del algoritmo de Búsqueda Tabú
A continuación se presentan los detalles de
diseño sobre la representación de datos y estructuras utilizadas para realizar
la implementación del algoritmo de Búsqueda Tabú al problema a tratar.
Representación de la información
·
Pedido: Un pedido tiene un tamaño, un
domicilio, una ventana horaria dentro de la que debe realizarse la entrega y un
ángulo respecto al centro de distribución.
·
Ruta: Una ruta es una secuencia
ordenada de pedidos donde el orden de los mismos se corresponde con el orden de
entrega. También incluye datos como su costo de acuerdo a la función de
evaluación y la amplitud angular respecto de los pedidos que la componen.
·
Movimiento: Es una estructura que
representa la transferencia de una secuencia de a lo sumo tres pedidos consecutivos, desde una ruta de origen hacia
una determinada posición en una ruta de destino.
·
ListaTabú: Es una secuencia de movimientos
y se la utiliza para almacenar aquellos movimientos que son tabú y no pueden
ser realizados.
·
Solución: Representa una solución
factible al conjunto de datos que definen la instancia del problema con el que
se está trabajando. Esta estructura es alterada por la metaheurística a través
de la aplicación de movimientos en el proceso de Búsqueda Tabú. Como
información propia posee la lista de rutas que definen los recorridos a
realizar para la entrega de los pedidos ingresados en el sistema y su costo de
acuerdo a la función de evaluación.
Elementos
de la Búsqueda Tabú
Lista Tabú
El objetivo principal de la Lista Tabú es
evitar que la metaheurística se quede trabada en un mínimo local. Esto lo logra
permitiendo al algoritmo salir de los mínimos locales mediante la prohibición
de realizar los movimientos más recientes que lo llevarían nuevamente al mínimo
local. Esta lista se encuentra representada por una lista enlazada de
movimientos. En lugar de almacenar los movimientos que fueron aplicados
recientemente, se utiliza el método de guardar los movimientos inversos a los aplicados. De este modo antes de
aplicar un nuevo movimiento a la solución actual basta con verificar si ese
movimiento aparece en la lista tabú. En caso de aparecer significaría que ese
movimiento posiblemente lleve a visitar una solución que fue visitada en otra
iteración reciente de la búsqueda.
Criterio de parada
Debido al dinamismo que se plantea en el
problema a tratar, y a que se espera que el algoritmo genere soluciones
aceptables en lapsos de tiempos muy cortos se decidió no utilizar como criterio
de parada la habitual cota de cantidad de iteraciones, y se empleó una cota
basada en tiempo de ejecución lo cual permite que el algoritmo satisfaga la característica
de sistema on-line independientemente de la velocidad de la computadora donde
se lo ejecuta.
Movimiento
Como se explicó anteriormente y de acuerdo
a la estrategia seleccionada de exploración del espacio de soluciones, un
movimiento consiste en el pasaje de hasta tres pedidos consecutivos desde una
ruta de origen hacia algún punto dentro de una ruta de destino.
La aplicación de un movimiento es una
operación atómica y un movimiento es válido si y solo si luego de su aplicación
a una solución factible produce una nueva solución también factible.
Definición del vecindario
Resumiendo lo explicado en las secciones
anteriores, la vecindad consiste en seleccionar en forma aleatoria dos
conjuntos de rutas, siendo uno las rutas que serán consideradas rutas de origen
y el otro conjunto las rutas de destino. Cada conjunto de rutas cumple la
restricción de tener como máximo t pedidos. Es posible que los conjuntos de
origen y destino tengan elementos en común y esto significa que se analizarán
los movimientos que se puedan realizar entre los pedidos de una misma ruta.
Luego, la vecindad son todos los
movimientos factibles desde cada ruta de origen a todas las rutas de destino
siempre y cuando sus radios de acción se intersecten. Este uso del radio de
acción permite limitar enormemente la cantidad de movimientos a analizar en
caso de que las rutas seleccionadas tengan orientaciones muy disímiles. Los
movimientos a realizar consisten en los intercambios Or-Opt detallados al principio del capítulo. Esta vecindad tiene
tamaño O(t2) y es polinomial respecto a la cantidad de pedidos a
analizar.
Manejo de múltiples soluciones
Una de las optimizaciones realizadas a la
Búsqueda Tabú tal como se explicó en secciones anteriores fue el agregado del
manejo de múltiples soluciones candidatas.
El algoritmo explora la vecindad de la
solución que intenta optimizar mientras no se cumpla el criterio de parada que,
como se explicó anteriormente, es un intervalo o quanto de tiempo. El análisis
de la vecindad implica realizar todos los movimientos de mejora posibles y la
máxima cantidad de movimientos de no mejora permitidos. En caso de lograr
explorar toda la vecindad de la solución antes de terminar de utilizar el
quanto de tiempo se utiliza el tiempo restante para optimizar otra solución distinta. Esa nueva solución
distinta se genera insertando en orden aleatorio los pedidos que hay en el
sistema dentro de una solución vacía.
De este modo el algoritmo mantiene un
conjunto acotado de soluciones candidatas, cada solución está dotada de un
costo que es el valor que se desea optimizar y se toma como solución principal a aquella con menor costo
dentro de las soluciones candidatas.
En cada quanto de tiempo destinado a
optimización se explora la vecindad de la solución principal, en caso de sobrar
tiempo se explora la vecindad del resto de las soluciones candidatas analizándolas
en el orden en que fueron creadas mediante un mecanismo de round-robin. De este
modo se emplea la mayor cantidad de tiempo en la solución más prometedora y
luego se utilizan los sobrantes en soluciones que tienen condiciones para ser
soluciones principales.
Intensificación de la búsqueda
El mecanismo de intensificación está
instrumentado a través del manejo de múltiples soluciones y el criterio
utilizado para seleccionar qué solución candidata será la siguiente en ser
optimizada. El hecho de analizar prioritariamente la solución principal (que es aquella solución
conocida que tiene el menor costo) sirve como mecanismo de intensificación
debido a que se está analizando con mayor detalle la vecindad de la misma.
Diversificación de la búsqueda
En forma análoga a la intensificación, este
mecanismo se lleva a cabo a través del manejo de múltiples soluciones. El hecho
de generar y mantener un conjunto de soluciones
candidatas que se exploran secuencialmente hace que la exploración del
espacio de soluciones se diversifique en distintas vecindades. Generando así oportunidades
para encontrar óptimos locales en la vecindad de cada una de las soluciones
candidatas.
Función objetivo
La función objetivo es aquella cuyo valor
se desea minimizar, en este caso se adoptó una función que contempla los
siguientes aspectos de la solución en orden de prioridad:
·
Cantidad de rutas: Cantidad de rutas
que componen la solución. Se busca obtener la solución con menor cantidad de
vehículos utilizados.
·
Distancia: Longitud total de todas las
rutas necesarias para realizar la entrega de los pedidos. Se busca obtener la
solución con menor distancia a recorrer.
·
Tiempo de espera: Tiempo de espera
total en todos los recorridos. Se pretende minimizar los tiempos de espera
entre entregas de pedidos.
El peso relativo de los distintos aspectos es:
· Costo del uso de una ruta: 10.000 unidades
· Costo del recorrido de una unidad de distancia en la grilla: 1 unidad
· Costo de un minuto de tiempo en la simulación: 1 unidad
Capítulo
5: Implementación
El sistema desarrollado como prueba
conceptual de la heurística planteada está compuesto de tres módulos
principales: el dispatcher, el optimizador y la visualización. El módulo
dispatcher implementa el modelado del tiempo y la generación de eventos. El
módulo optimizador implementa la metaheurística y el manejo de múltiples
soluciones y el módulo de visualización permite comunicar al usuario el
resultado de la simulación que se está corriendo.
En este capítulo se describen algunos
detalles de la implementación de los distintos módulos que componen el sistema,
de su interacción y de su funcionamiento, como así también consideraciones
generales del desarrollo. Además se detallan algunas de las características
técnicas como el lenguaje de programación utilizado, las máquinas sobre las que
se realizo el sistema y el formato de algunos de los archivos necesarios para
la configuración.
Consideraciones
generales de la implementación
Dinamismo y simulación de eventos en lote (batch)
Como se describió en los capítulos
anteriores, el objetivo principal de la tesis es plantear una heurística para
la optimización del problema de ruteo de vehículos con pedidos que ingresan
dinámicamente. Esto implica que el conjunto total de pedidos no es conocido de
antemano sino que va siendo modificado con el tiempo y el surgimiento de distintos
eventos (entrada de nuevos pedidos, salida de vehículos, etc.).
Poder manejar estos eventos de forma
dinámica plantea una dificultad importante a la hora de realizar pruebas, ya
que hace necesaria la presencia de un operador humano o un agente que se encargue
de informar los distintos eventos al sistema. No siendo viable la opción de
depender de un operador humano, ya sea por el volumen de datos o por el tiempo
mismo que demora la corrida de un lote de prueba se decidió implementar un
sistema automático para la simulación y procesamiento de los eventos, esta
tarea es la principal función del módulo dispatcher.
Un problema adicional que surge al
introducir el concepto de simulación es que al estar pensada para realizarse en
tiempo real, cada corrida demoraría tanto como la amplitud horaria en la que se
desarrollen sus eventos. Por este motivo, se dotó al dispatcher de un mecanismo
para escalar el intervalo horario de la simulación y poder transformarlo en
otro más acotado. De este modo, una simulación que cubre un lapso de tiempo de
cuatro horas puede realizarse en un período mucho más corto y a discreción del
usuario, pudiendo ser por ejemplo diez minutos.
La implementación realizada del ingreso de
los eventos en lote se hizo en base a un archivo de configuración (cuyo formato
se verá más adelante) y un módulo que lo interpreta y ejecuta. Sin embargo,
queda planteado como trabajo futuro la implementación de una interfaz gráfica
que permita la interacción en tiempo real de un operador con el sistema para poder
usar el mismo en entornos reales de producción. Es importante destacar que para
el desarrollo de la aplicación se tuvo el cuidado de permitir la incorporación
de una futura interfaz gráfica evitando el acoplamiento entre los módulos de
procesamiento de la simulación y los de ingreso de eventos.
El
módulo dispatcher
El dispatcher es el módulo responsable de
leer e interpretar el archivo de simulación y de transmitir los distintos
eventos que encuentra en el mismo al módulo optimizador.
El funcionamiento del dispatcher empieza
con la lectura e interpretación (parseo) del archivo de simulación. Mientras lo
va interpretando, crea una lista de objetos que representan los distintos tipos
de eventos y la hora en la que deben suceder. Además de ser el contenedor de
eventos, la función principal del dispatcher consiste en implementar el método
ProximoEvento(). Este método verifica la hora actual en la que se encuentra la
simulación y entrega todos los eventos que hayan sucedido desde la última vez
que se lo invocó. La hora actual de la simulación es mantenida por el objeto
Reloj cuyo principal método es Hora().
Otra función importante del dispatcher
consiste en implementar la política de salida de rutas que es el mecanismo por
el cual se simula la decisión del usuario de indicar que parta un vehículo a
distribuir los pedidos contenidos en una determinada ruta. La verificación de
la política de salida de rutas se realiza cada vez que se invoca el método
ProximoEvento().
Eventos
El sistema maneja distintos tipos de eventos.
Cada uno de ellos representa una acción externa sobre el sistema o bien eventos
internos generados por el mismo. Cada tipo de evento está definido por una hora
en la que debe suceder dentro de la simulación y un conjunto de datos
complementarios. Los tipos de eventos que maneja el sistema son:
·
EventoAgregarPedido(Pedido):
Representa la entrada de un nuevo pedido al sistema.
·
EventoRemoverRuta(Ruta): Representa la
partida de un vehículo del depósito para realizar la entrega de los pedidos
asociados a una ruta.
·
EventoSetearParametro(Parametro,
Valor): Se lo utiliza para modificar parámetros del sistema.
·
EventoFin(): La ejecución de este
evento implica el fin de la simulación.
El evento EventoRemoverRuta no puede
aparecer dentro de un archivo de simulación puesto que cuando se está diseñando
la misma no es posible saber en que momento una ruta estará lista para su
partida. Detalles sobre la generación de este evento pueden verse en la sección
política de Salida de Rutas.
Los eventos que conforman una simulación
son almacenados en un archivo de configuración en formato XML que es leído e
interpretado por el módulo dispatcher. El formato XML de un evento sigue el
siguiente esquema:
<evt id="00"
horarelativa="11" tipo="EvtAgregarPedido">
Todos los eventos poseen como datos mínimos
un identificador único (id), una hora relativa en la que deben ser ejecutados
dentro de la simulación y un tipo. El tipo, además de marcar la clase del
evento, también fija los datos adicionales que deberá especificar. A modo de
ejemplo, los eventos de tipo “EvtAgregarPedido” deben especificar todos los
datos del pedido que se desea ingresar.
Sequencer
El sequencer se encarga de simular el
avance del tiempo actualizando la hora contenida en el Reloj de la simulación
hasta llegar al evento que indica el final de la misma. Acá es donde se
implementa el ciclo principal del sistema para simular todos los eventos que
conforman una corrida.
Simular()
evento = Dispatcher.ProximoEvento();
Mientras no sea el evento de Fin
Si no hay ningún evento a ejecutar
ActualizarReloj(IntervaloAvanceSequencer)
Optimizador.Optimizar(IntervaloAvanceSequencer)
Sino
evento.Ejecutar
Fin si
evento = Dispatcher.ProximoEvento();
Como se puede ver en el pseudocódigo
presentado, cada iteración del método se encarga de consumir y ejecutar los
eventos almacenados en el dispatcher para la hora actual de la simulación en
caso de haberlos. En caso contrario, actualiza el Reloj incrementando la hora
actual en la cantidad de ticks contenida en la constante IntervaloAvanceSequencer.
De este modo la simulación transcurre en
intervalos de tiempo discretos en los que se permite al módulo optimizador
repartir ese quanto de tiempo entre las distintas etapas que componen la
optimización de las soluciones.
Política de salida de rutas
Dado que el sistema realiza una simulación
de la entrada de pedidos, es necesario contar con un mecanismo que permita
decidir en qué momento un recorrido se encuentra lo suficientemente optimizado
como para indicar la partida de un vehículo que realice dicha ruta de entregas.
Realizar este cálculo es un problema sumamente complejo que incluso pareciera
no tener solución exacta ya que uno no puede predecir a priori si un nuevo
pedido que podría entrar en el futuro generaría una asignación mejor de los
pedidos en las rutas.
En la realidad un operador humano debería
revisar las rutas informadas por el sistema a través de su interfaz gráfica y
en base a una serie de consideraciones propias del negocio decidir en que
momento una ruta debe ser efectivamente realizada por un vehículo. Por supuesto
que esta decisión debe realizarse con anticipación suficiente como para que se
pueda satisfacer la entrega del pedido
que venza más temprano en la ruta que se pretende efectuar.
Para sustituir a un operador humano y hacer
viable la simulación como mecanismo de prueba automatizado del sistema, se
implementó un algoritmo que inspecciona las rutas contenidas en la mejor
solución conocida hasta el momento y utilizando un criterio determinístico
selecciona aquellas que deben ser removidas del sistema y llevadas a cabo por
un vehículo.
Los distintos criterios que se evaluaron a
la hora de implementar el algoritmo para decidir la partida de una ruta fueron:
·
Cuando tenga cierto porcentaje de
ocupación en el espacio de carga del vehículo asignado a la misma, o bien
cuando falte cierta cantidad de minutos para el momento en que la ruta dejará
de ser factible.
·
Cuando tenga cierto porcentaje de
ocupación en el espacio de carga del vehículo asignado a la misma y además su
radio de acción se superponga en cierta medida con el radio de acción de otras
rutas, o bien cuando falte cierta cantidad de minutos para el momento en que la
ruta dejará de ser factible.
·
Cuando falten X minutos para el
momento en el que la ruta dejará de ser factible.
Como se puede apreciar, se desprende de la
lista anterior que un factor constante a tener en cuenta al momento de decidir
la partida de una ruta en los tres criterios es el tiempo más tardío en el que
un vehículo debe partir del depósito para lograr cumplir con las entregas en
las bandas horarias planificadas. Ese límite implica que la partida en un
momento posterior no da tiempo suficiente al vehículo para cumplir con al menos
una de las ventanas horarias de los pedidos que componen la ruta. Es por esto
que es indispensable incluir esa condición en cualquier criterio que se
proponga.
Analizando ahora más detalladamente, vemos
que en el primer criterio se está tomando una postura optimista ya que
suponemos que una ruta está bien planificada tan pronto como se logre ocupar
una cierta cantidad del espacio de carga de su vehículo. Esto podría ser útil
en casos donde el volumen de pedidos ingresados en el sistema sea realmente muy
alto y el tiempo empleado para realizar la optimización deba distribuirse entre
una cantidad muy grande de pedidos, siendo aceptable conformarse con un
determinado nivel de ocupación. Sin embargo, se está pasando por alto que la
distribución espacial o temporal de los pedidos asignados a la ruta podría ser
muy mala. Por ejemplo, podría contener pedidos ubicados a mucha distancia entre
sí o pedidos sucesivos para los que haya mucho tiempo de espera entre sus
entregas.
El segundo criterio incluye al primero pero
además propone tener en cuenta la superposición del radio de acción de las
rutas, siendo prioritaria la salida de rutas que tengan radios de acción
solapados. Se supone que en caso de haber varias rutas que recorran zonas
similares y que no se hayan podido unir en una sola, es conveniente efectuar
las entregas de una de esas rutas a fin de minimizar el tiempo de espera de los
clientes. En caso de que posteriormente entraran pedidos para esa zona se
espera que se puedan acomodar dentro de las otras rutas que cubrían esa misma
área de entrega.
El
tercer criterio se basa en la simplificación de las condiciones y
propone permitir que la optimización de las rutas continúe hasta el momento más
tardío posible. De este modo las rutas son sometidas a optimización hasta el último
momento con la intención de que un mayor tiempo de permanencia dentro del
sistema les permita mejorar su calidad, ya sea realizando intercambios de
pedidos con otras rutas o bien incorporando pedidos recién ingresados al
sistema que pueden aprovechar un recorrido que está por partir.
En las primeras implementaciones del
sistema fuimos probando los distintos criterios. Sin embargo fue el último el
que brindó los mejores resultados y el que decidimos usar para la versión
final. Creemos que es la combinación de simplicidad y la oportunidad de
realizar y analizar mayor cantidad de intercambios lo que hace del tercer
criterio el mejor.
Parámetros de una simulación
Algunos parámetros del sistema pueden ser
configurados para cada simulación en particular, a continuación se detallan
dichos parámetros y una descripción de su propósito:
·
Reloj.Hora: Es la hora que marca el
reloj de la simulación al comenzar la misma.
·
DomicilioDeposito: Son las coordenadas
(x, y) donde está ubicado el centro de distribución.
·
HoraFinalizacionEntrega: Es la hora
más tardía en la que se admite la entrega de un pedido en un cliente.
·
CapacidadVehículo: Indica la capacidad
máxima de transporte de los vehículos de la flota.
·
AmplitudRadioDeAccion: Es la máxima
amplitud angular que puede tener cada ruta en su radio de acción.
·
SemillaRandom: Es la semilla empleada
en la generación de números pseudoaleatorios.
·
MaximaCantidadDiversificaciones:
Máximo número de diversificaciones realizadas durante la ejecución del
algoritmo de búsqueda Tabú.
·
CoeficienteDistanciaATiempo: indica
cómo es la relación para la conversión de la distancia total de las rutas a una
unidad de tiempo de forma tal de poder utilizar ambos valores para calcular los
costos
·
UsarMinutosParaDistanciaATiempo:
indica qué unidad de tiempo se utiliza (minutos o segundos) para los cálculos
de tiempos de espera
·
IntervaloAvanceSequencer: Indica la
granularidad medida en ticks con la que avanza el reloj del sistema
·
SegundosParaVencimientoRuta: Indica a
la política de salida de rutas con qué anticipación debe indicar la salida de
un vehículo para efectuar una ruta, teniendo como referencia el momento en que ésta
se vence.
Formato de los archivos de simulación
Cada simulación está definida por un
archivo XML que contiene los valores para los distintos parámetros del sistema
y una secuencia de eventos ordenados cronológicamente que representan la
entrada de pedidos.
Archivo de ejemplo
A continuación se presenta a título
ilustrativo el contenido de una simulación muy breve:
<?xml version="1.0"
encoding="iso-8859-1" ?>
<eventos directorioSVGs="E:\WorkingCopies\Facu\Tesis\trunk\code\Tests\Tests\">
<!-- Seteo
de parámetros iniciales -->
<evt
id="0" horarelativa="null"
tipo="EvtSetearPametro" nombreP="HoraInicial"
valorP="19:00:00" />
<evt
id="1" horarelativa="null"
tipo="EvtSetearPametro" nombreP="Reloj.Hora"
valorP="19:00:00" />
<evt
id="2" horarelativa="null"
tipo="EvtSetearPametro" nombreP="DomicilioDeposito"
valorP="40,50" />
<evt
id="3" horarelativa="null"
tipo="EvtSetearPametro" nombreP="HoraFinalizacionEntrega"
valorP="1236" />
<evt id="4"
horarelativa="null" tipo="EvtSetearPametro"
nombreP="CapacidadVehículo" valorP="200" />
<evt
id="5" horarelativa="null"
tipo="EvtSetearPametro" nombreP="AmplitudRadioDeAccion"
valorP="70" />
<evt
id="6" horarelativa="null" tipo="EvtSetearPametro"
nombreP="SemillaRandom" valorP="1" />
<evt
id="7" horarelativa="null"
tipo="EvtSetearPametro"
nombreP="MaximaCantidadDiversificaciones" valorP="1" />
<evt
id="8" horarelativa="null"
tipo="EvtSetearPametro"
nombreP="CoeficienteDistanciaATiempo" valorP="1" />
<evt
id="9" horarelativa="null"
tipo="EvtSetearPametro"
nombreP="UsarMinutosParaDistanciaATiempo" valorP="false"
/>
<!--
Intervalo de incremento del sequencer en segundos (este es el tiempo que le va
dando al optimizador -->
<evt
id="10" horarelativa="null"
tipo="EvtSetearPametro" nombreP="IntervaloAvanceSequencer"
valorP="60" />
<evt
id="10" horarelativa="null"
tipo="EvtSetearPametro"
nombreP="SegundosParaVencimientoRuta" valorP="120" />
<!-- Fin
seteo de parámetros iniciales -->
<evt id="10"
horarelativa="0" tipo="EvtAgregarPedido">
<pedido
id="1" tamano="10" inicioventana="912"
finventana="967" x="45" y="68" />
</evt>
<evt
id="11" horarelativa="10"
tipo="EvtAgregarPedido">
<pedido
id="2" tamano="20" inicioventana="930"
finventana="1067" x="60" y="60" />
</evt>
<evt
id="99999" horarelativa="1000"
tipo="EvtFinSimulacion" />
</eventos>
El
módulo optimizador
El módulo optimizador es el encargado de
organizar y mantener las distintas soluciones candidatas que está analizando el
sistema. Entre sus responsabilidades se encuentran las de crear y mantener
referencias a las soluciones candidatas, así como implementar el algoritmo que
selecciona la siguiente solución a optimizar por la metaheurística. Su
principal método es Optimizar(intervalo) cuyo pseudocódigo de su algoritmo se
ve a continuación.
Optimizar(intervalo)
solución = MejorSolucionConocida
Metaheuristica.Optimizar(solución, intervalo)
Actualizar el intervalo de tiempo restante
Mientras no se haya consumido el intervalo de
tiempo restante
Tomar como solución una solución candidata en
orden Round-Robbin
Metaheuristica.Optimizar(solución,
intervaloRestante)
Si el costo de la solución es menor al de
MejorSolucionConocida
MejorSolucionConocida = solución
Actualizar el intervalo de tiempo restante
Como puede verse es prioridad del
Optimizador aplicar la metaheurística a la mejor solución conocida hasta el
momento, con la intención de que una intensificación en la exploración
realizada en la vecindad de la misma arroje soluciones cada vez mejores. Una
vez terminada la eventual mejora de la mejor solución se destina el tiempo
restante (en caso de que lo haya) para optimizar el resto de las soluciones
candidatas tomándolas en un orden Round Robbin. De esta forma se pretende lograr
una diversificación en la búsqueda de soluciones. En caso de que una de las
soluciones candidatas obtenga un costo menor que el de la mejor solución
conocida, la primera pasa a convertirse en la nueva mejor solución.
Metaheurística
Dentro del optimizador, el submódulo de la
metaheurística implementa el algoritmo de búsqueda tabú y la optimización local
entre rutas. Este submódulo fue realizado con una interfaz general que permite
su reemplazo por otros submódulos que implementen distintas metaheurísticas
para resolver el problema de la optimización. Otro trabajo futuro que se
desprende de esta tesis es la realización de varios submódulos que implementen
distintas metaheurísticas y la comparación entre los resultados obtenidos por
todos ellos. Al igual que sucede con el método principal del optimizador, la
función principal de la metaheurística está gobernada por un intervalo de
tiempo durante el cual se permite que el algoritmo realice su trabajo de buscar
las posibles optimizaciones. A continuación se presenta el algoritmo
implementado de búsqueda tabú:
Optimizar(solución,
intervalo)
solucionAOptimizar = solución
//Diversificaciones
Mientras quede tiempo y no se hayan realizado
todas las diversificaciones
// Optimización local
Mientras quede tiempo y No se cumpla el
criterio de parada
// Mejor Movimiento + Mejor entre 2 rutas
Por cada movimiento en el vecindario
Si no está en la lista Tabú o cumple con el
criterio de Aspiración
Si la mejora obtenida por el movimiento
supera un determinado %
mejorMovimiento = movimiento
Salir del Por
Sino
solucionTemporal = movimiento.AplicarEn
(solucionAOptimizar)
Si solucionTemporal.Costo <
solucionAOptimizar.Costo
mejorMovimiento = movimiento
Fin Si
Fin Si
Fin Si
Fin Por
solucionTemporal = mejorMovimiento.AplicarEn
(solucionAOptimizar)
Si solucionTemporal.Costo <
solucionAOptimizar.Costo
solucionAOptimizar = solucionTemporal
Fin Si
Fin Mientras
Si solucionAOptimizar.Costo < solucion.Costo
solución = solucionAOptimizar
Fin Si
solucionAOptimizar =
Diversificar(solucionAOptimizar)
Fin Mientras
El algoritmo está formado por dos ciclos principales
anidados. El externo realiza el control del tiempo usado por el algoritmo de
modo de no exceder el quanto asignado para la ejecución de la metaheurística y a
la vez lleva el control de la cantidad de diversificaciones que se aplican.
Cada diversificación está implementada como
un reingreso en un orden aleatorio de todos los pedidos incluidos en el
sistema. Está acción combinada con el algoritmo de inserción de pedidos
explicado anteriormente permite generar nuevas soluciones con una asignación
aleatoria de pedidos por cada ruta y asegura que la nueva solución generada es
válida.
El ciclo interno implementa la búsqueda
local y utiliza como criterio de parada una determinada cantidad de
aplicaciones de movimientos tabú que no hayan producido mejora. Dentro del
cuerpo de este ciclo se realiza la exploración de los posibles movimientos definidos
en la vecindad de la solución actual.
Recordemos que un movimiento consiste en la transferencia de uno, dos o tres
pedidos consecutivos desde una ruta de origen a una ruta destino.
Probamos varios métodos distintos para la
exploración de la vecindad. Sin embargo, algunos, aunque producían resultados
satisfactorios para conjuntos relativamente pequeños de pedidos, no resultaban
escalables. Uno ejemplo de esto es el último método que utilizamos durante el
desarrollo antes de llegar al algoritmo final. Este método realizaba un
ordenamiento de todas las rutas de acuerdo a la cantidad de pedidos que la
componían y al nivel de ocupación de la capacidad de cada vehículo. Las rutas
de origen eran ordenadas de menor a mayor de acuerdo a la cantidad de pedidos que
las componían. La intención de este ordenamiento era permitir que rutas con
pocos pedidos quedaran “vacías” eliminándose del conjunto de rutas. Las rutas
de destino se ordenaban de menor a mayor de acuerdo al espacio utilizado de su
capacidad de transporte. En este caso, se buscaba priorizar como rutas
receptoras de pedidos aquellas que tenían menor cantidad de espacio utilizado y
se basaba la suposición de que las rutas con cierto índice de ocupación de su
capacidad de transporte estaban lo suficientemente llenas como para priorizar
la exploración de movimientos en otras rutas menos ocupadas. Una vez realizados
los dos ordenamientos del conjunto de rutas, se tomaban todos los pares de
rutas de origen y destino analizando los posibles movimientos entre cada par de
rutas.
Al subir la cantidad de pedidos
considerablemente, ya no se hacía factible buscar los posibles movimientos
entre todos los pares de rutas por lo que era necesario tomar un subconjunto de
rutas de origen y otro de destino para chequear los movimientos sólo entre éstas.
Esta necesidad de recortar los conjuntos analizados de origen y destino nos
forzó también a tener que descartar el ordenamiento ya que en las pruebas que
hicimos con el mismo obteníamos resultados claramente muy malos debido a que
una vez que el ordenamiento planteado nos dejaba dos conjuntos de rutas de
origen y de destino que no poseían intercambios que mejorasen la solución, el
único avance posible era pasar a una diversificación. Sólo descartando el
ordenamiento y realizando la selección de los conjuntos de rutas a utilizar
como origen y destino de manera aleatoria pudimos obtener los muy buenos
resultados finales que presentamos más adelante.
Continuando con la descripción del
algoritmo, una vez obtenido un movimiento de mejora, se analiza si esta mejora
obtenida representa un porcentaje de disminución significativo sobre el costo
de la solución. En caso de serlo, se toma ese movimiento como el mejor
movimiento. Si no lo es, se sigue buscando al mejor movimiento del vecindario
analizando las mejoras en los costos. Cabe aclarar que sólo son tenidos en
cuenta los movimientos que no se encuentran en la lista Tabú o que cumplen con
el criterio de aspiración
Finalmente de acuerdo a si la aplicación
del mejor movimiento a la solución actual genera una solución de menor costo
que la mejor solución conocida, se realiza el reemplazo de ésta por la nueva
generada.
El
módulo de visualización
En un primer momento los resultados de las
corridas del sistema eran analizados a través del archivo de log que generaba
el programa. Sin embargo, la representación textual de los datos no permitía
analizar a simple vista la validez de las rutas generadas ni comprender
cabalmente cuales eran los distintos cambios que iba produciendo el algoritmo
en la solución. Por esto decidimos la implementación del módulo de
visualización. La generación de las imágenes se realizó utilizando el formato
de archivos SVG (Scallable Vector Graphics) que permiten la representación de
elementos gráficos vectoriales en forma de texto XML. Este es luego
interpretado por un motor que se encarga de realizar la representación gráfica
del archivo.
A continuación se muestra a modo de ejemplo
una pequeña secuencia de una corrida del sistema
: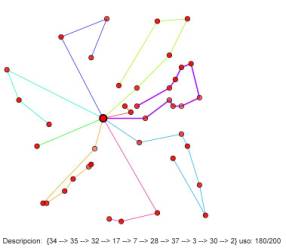
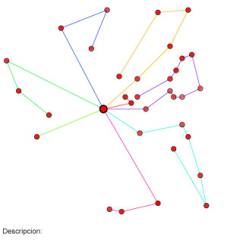
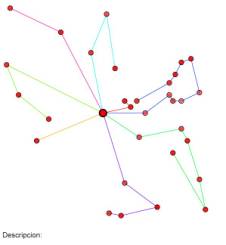
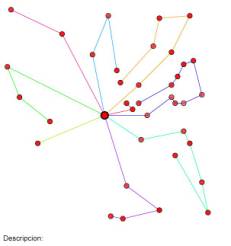
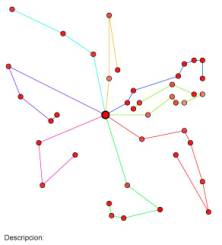
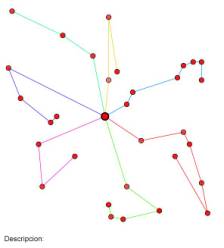
Si se observa en detalle los gráficos se
puede notar como va variando la solución a medida que transcurre el tiempo y
que ingresan nuevos pedidos y salen rutas.
Las referencias utilizadas para la
representación visual son las siguientes:
·
El espacio de visualización es un eje
de coordenadas (x, y) que representa el mapa simplificado de la zona de
entregas.
·
Un punto distinguido de mayor diámetro
representa el depósito central desde donde parten todos los vehículos a
realizar las entregas.
·
El resto de los puntos y su ubicación
dentro del mapa representan los pedidos de entrega que deben realizarse.
·
Cada pedido brinda información sobre
la ventana de tiempo en que debe realizarse la entrega y sobre la ventana de
tiempo estimada por el sistema en que se realizará dicha entrega.
·
Se utiliza la intensidad del color
rojo para representar en cada pedido el tiempo que falta para su vencimiento. A
mayor intensidad de color, menor tiempo falta para su vencimiento.
·
Las líneas rectas de un mismo color
representan el recorrido de una ruta, las cuales parten del depósito y terminan
en él. Para simplificar la visualización se omite la representación del tramo
que une la entrega del último pedido de una ruta con el depósito central.
La visualización es la forma en la que el
usuario puede obtener información acerca del resultado de la simulación. Dado
que las soluciones que maneja el sistema pueden variar mucho en un intervalo de
tiempo muy chico, encontramos que era conveniente generar una foto del conjunto de rutas que componen la
solución actual únicamente cuando un vehículo que tiene asignada una ruta va a
partir e inmediatamente después de que el vehículo y los pedidos fueron
removidos de la solución. De ésta manera se facilita poder apreciar cuál es la
ruta que se removió del sistema y la (eventual) nueva asignación de pedidos a
las rutas restantes.
Por lo tanto, el resultado de la corrida de
una simulación es una secuencia de archivos SVG donde cada uno representa el
estado de las rutas que componen la mejor solución conocida en cada momento de
la simulación. Cada archivo contiene la hora de la simulación en la que se tomó
la información de modo que las imágenes pueden ser ordenadas en función del
momento en que fueron tomadas y presentadas al usuario en orden cronológico.
Para presentar los archivos SVG al usuario
se diseñó un aplicativo HTA (HTML for Applications) capaz de realizar las
tareas básicas de browsing de imágenes. Este aplicativo puede ser utilizado en
cualquier navegador de Internet que soporte este tipo de formatos.
Lenguaje
y metodología
Para la implementación del sistema decidimos
utilizar el lenguaje C# de Microsoft en su versión 1.1. La elección se basó en
la experiencia con la que contamos en este lenguaje y la facilidad del mismo
para desarrollar sistemas orientados a objetos.
El desarrollo de la tesis pasó por las
etapas típicas de cualquier proyecto comercial. Primero realizamos el
relevamiento de las necesidades reales
del sistema. En la segunda etapa realizamos el análisis y el diseño empezando
por diagramas más generales y yendo hacia lo más particular. Utilizamos diagramas
de Objetos, de Clase y de Interacción para reflejar los distintos aspectos del
sistema y poder contar con una idea bastante detallada de la futura
implementación.
Hardware
y Sistema Operativo
Para el desarrollo y las pruebas se utilizo una PC Duron de 2000+ con 1 Giga de memoria RAM. El sistema operativo sobre el cual se trabajó fue Windows 2003 Enterprise Server.
Capítulo
6: Resultados obtenidos
A
continuación se presentan los resultados obtenidos al aplicar la heurística
propuesta a una variedad de conjuntos de datos de entrada.
Lotes
de prueba
Para poder evaluar el desempeño del
algoritmo implementado se intentó obtener algún conjunto de datos de entrada
standard con el cual poder comparar los resultados. Esta tarea no tuvo éxito ya
que no pudimos encontrar ninguna instancia del problema ruteo de vehículos con
ventanas de tiempo on-line (VRPTW online). Sí logramos encontrar instancias de
prueba para el problema de ruteo de vehículos (VRP) y para su variante con ventanas
de tiempo (VRPTW). Sin embargo, como se explicó anteriormente, en este tipo de
problemas el conjunto de pedidos se conoce inicialmente y no se incrementa con
el tiempo. La variante estática del problema puede verse como un caso
particular de la versión online si se considera que todos los pedidos ingresan
en el primer instante de tiempo y que no aparecen nuevos hasta el final de la
ejecución del algoritmo. Por lo tanto se utilizó una serie de estas instancias
como primer medida de comparación para el funcionamiento de la heurística. Posteriormente
fue necesario implementar una herramienta para generar instancias de prueba en
la que los pedidos ingresaran a medida que transcurre el tiempo. Esta
herramienta permitió generar una gran cantidad de instancias donde los pedidos
tuvieran una distribución aleatoria tanto temporal como espacial.
Instancias
propuestas por Solomon
Una de las primeras dificultades que
encontramos fue resolver de qué manera comparar los resultados obtenidos por
nuestro algoritmo con las mejores soluciones conocidas a las instancias de
prueba de Solomon [SOL]. Inicialmente utilizamos algunas instancias de VRP las cuales están
representadas sobre un eje de coordenadas (x, y) y cuya métrica utilizada para
la calidad de una solución es la distancia total recorrida por el conjunto de
rutas que la componen. Tomando en consideración esto, modificamos la función de
evaluación de la heurística para priorizar la optimización de la distancia
recorrida y la cantidad de rutas generadas, dejando de lado momentáneamente la
optimización de las ventanas de tiempo. De esta manera las soluciones obtenidas
con nuestra heurística eran comparables con las mejores soluciones que se
conocen a las instancias de prueba en cuestión. La intención de estas pruebas
era verificar que independientemente de las ventanas de tiempo nuestro
algoritmo generaba un conjunto de rutas que minimizara la distancia recorrida y
la cantidad de rutas utilizadas.
A continuación se presentan los resultados
obtenidos para distintos lotes de prueba:
|
|
Mejor
solución |
Solución
obtenida |
|
||
|
Instancia |
Rutas |
Distancia |
Rutas |
Distancia |
%
diferencia en distancia |
|
C101.100 |
10 |
827.3 |
11 |
876.5 |
6% |
|
C107.100 |
10 |
827.3 |
11 |
891.4 |
8% |
|
R101.100 |
20 |
1637.7 |
24 |
1821.4 |
11% |
|
R102.100 |
18 |
1466.6 |
20 |
1669.1 |
14% |
|
Tabla 01. Comparación en valores absolutos
y porcentaje de los resultados de las simulaciones realizadas con datos
standard |
|||||
Examinando los valores obtenidos se aprecia
que no se obtuvieron soluciones muy alejadas del mejor valor conocido, en
promedio la desviación respecto al mejor valor es menor al 10%. Como las instancias conseguidas no
correspondían al objetivo central de la optimización on-line, decidimos no
realizar más pruebas con esos conjuntos de datos.
Posteriormente se utilizaron instancias de
prueba de VRPTW estático. En este caso encontramos cierta similitud en la
configuración de las rutas obtenidas por medio de nuestra heurística y las
rutas de las mejores soluciones conocidas. En general esta similitud se
presentaba en la cantidad de rutas empleadas, o en alguna subsecuencia de
pedidos común a ambas soluciones. Sin embargo, los resultados que encontramos
solo priorizaban la distancia total recorrida por los vehículos sin tener en
cuenta la cantidad de vehículos utilizados. En nuestra implementación, siempre
fue el principal objetivo minimizar la cantidad de vehículos, por lo tanto los
valores obtenidos no pueden ser comparados.
Instancias
generadas en forma aleatoria
Como se mencionó anteriormente se generaron
tres lotes de instancias de prueba, utilizando un generador aleatorio que
implementamos. Las características de los distintos lotes se presentan a
continuación:
|
Lote |
Instancias |
Pedidos |
Mapa |
|
A |
200 |
60 |
50x50 |
|
B |
179 |
100 |
100x100 |
|
C |
54 |
350 |
100x100 |
|
Tabla 02. Comparación en valores absolutos
y porcentaje de los resultados de las simulaciones realizadas con datos
standard |
|||
Análisis de los resultados obtenidos
Partiendo de los distintos lotes de prueba
se realizaron varias observaciones para determinar el desempeño y funcionamiento de la heurística implementada. Una de
las primeras observaciones que realizamos fue analizar cuan lejos se encontraba
la cantidad de rutas generadas por el algoritmo de la mínima cantidad de rutas
que podría generarse en un caso ideal.
Consideramos como caso ideal de generación
de rutas aquel en el que los pedidos tienen todos el mismo tamaño y su
disposición espacial y temporal permiten que se los acomode de manera tal de
conseguir una ocupación total de la capacidad de cada vehículo. Este caso ideal
nos da una cota inferior en la cantidad de rutas que pueden utilizarse para
cumplir con todas las entregas. Por ejemplo para el caso de 10 pedidos en los
que cada uno tiene un tamaño de 2 unidades y los vehículos tienen una capacidad
de 4 unidades de transporte, podrían asignarse como máximo 2 pedidos a cada
vehículo. Luego, bajo las suposiciones del caso ideal la entrega podría
realizarse con un mínimo de 5 vehículos.
En la realidad la distribución espacial y
temporal de los pedidos condiciona fuertemente la viabilidad de agrupar pedidos
dentro de un mismo vehículo para su entrega. Por ejemplo, no es eficiente
ubicar en un mismo vehículo pedidos cuyas entregas deban realizarse en extremos
opuestos de la ciudad, este tipo de restricción aumenta notablemente la
cantidad mínima de vehículos con los que se puede realizar la entrega en forma
eficiente.
A continuación se analizan los resultados
para las distintas mediciones de la cantidad de rutas obtenidas para todos los
lotes de simulación.
Lote A, instancias de 60 pedidos
Para el lote de simulaciones de tamaño 60,
los pedidos tenían un tamaño promedio de 22 unidades (con un mínimo de 15 y un
máximo de 29) y la capacidad de los vehículos era de 200. Esto da un máximo
ideal de 9 pedidos por vehículo permitiendo la eventual generación de 7 rutas
distintas para satisfacer la entrega de todos los pedidos. En la figura 08 puede
apreciarse que sólo en muy pocas instancias nuestra implementación logra acercarse
a un mínimo de 8 rutas y en el caso promedio la cantidad utilizada ronda las
12. Esto se debe evidentemente a que la distribución espacial y temporal de los
pedidos difícilmente sea tal que permita realizar una ocupación total de cada vehículo
lo cual inevitablemente aumenta la cantidad de rutas a emplear. Además, los
pedidos cuentan con una ventana de tiempo que debe ser cumplida y muchos
vehículos deberán dejar el depósito antes de completar su capacidad de
transporte debido a restricciones temporales de los pedidos que transportan.
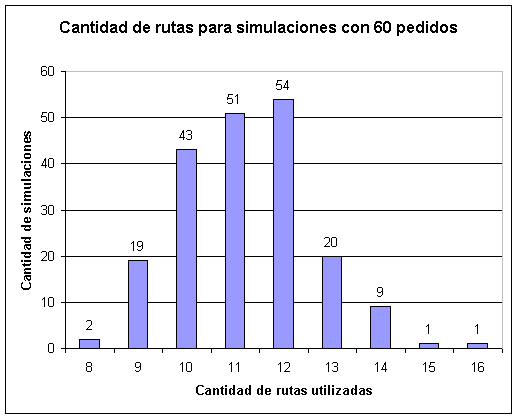
Fig. 08. Cantidad de rutas obtenidas por solución
para simulaciones con 60 pedidos
Cabe recordar para mejor interpretación del
gráfico que el lote está generado por 200 instancias distintas de 60 pedidos
cada una, con una asignación aleatoria de tamaños, dirección y ventanas de
tiempo.
Lote B, instancias de 100 pedidos
Para las instancias que contenían 100
pedidos, la asignación ideal a rutas permitiría realizar la entrega utilizando
12 vehículos. En este caso puede verse que los resultados obtenidos están muy
cerca de la cota mínima ya que en la mayoría de las simulaciones se logró
encontrar una solución que utilizara entre 12 y 13 rutas para la entrega. Esta
mejora en la performance puede atribuirse a dos factores, a que la elección de
la cota inferior posea un sesgo favorable a este tipo de instancias en
detrimento de las anteriores o a que al haber una mayor disponibilidad de
pedidos se permitió que los vehículos que debían partir por restricciones
temporales tuvieran un mejor índice de ocupación de su capacidad de transporte.
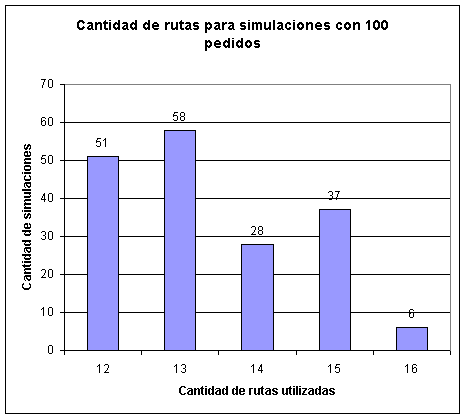
Fig. 09. Cantidad de rutas obtenidas por solución
para simulaciones con 100 pedidos
Lote C, instancias de 350 pedidos
El último lote de pruebas está compuesto
por instancias en la que se ingresan 350 pedidos con similares características que en los casos anteriores. La
cantidad mínima (ideal) de vehículos que podrían haberse empleado es de 39 y
puede observarse que la mayoría de las simulaciones utilizaron alrededor de 41
rutas para realizar la entrega. Los resultados obtenidos se alejan en promedio
un 4% de la cota inferior que difícilmente pueda darse en la realidad, esto
muestra el buen desempeño de la heurística implementada.
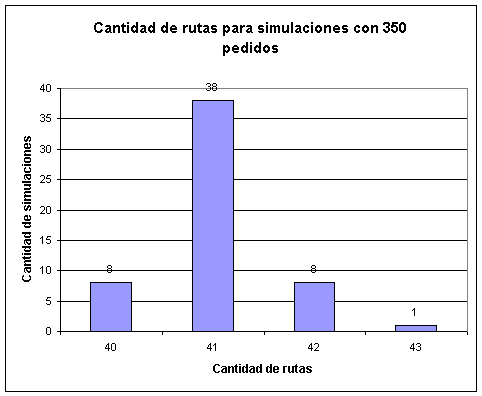
Fig. 10. Cantidad de rutas obtenidas por solución
para simulaciones con 350 pedidos
Análisis de la cantidad de rutas promedio utilizadas
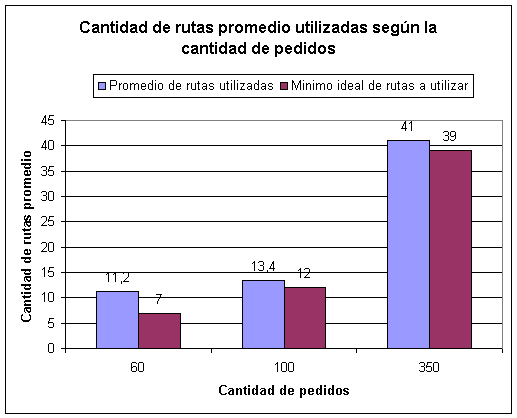
Fig. 11. Comparación de las rutas promedio utilizadas
y el mínimo ideal para los distintos tamaños de conjuntos de pedidos
Este gráfico representa el promedio
ponderado de rutas utilizadas en cada lote y permite comparar ese valor con el
mínimo ideal de rutas que podrían haberse utilizado en cada lote de acuerdo a
las suposiciones hechas al principio de esta sección para el caso ideal. Se puede
observar que en los dos últimos lotes los valores obtenidos se alejan muy poco
de ese mínimo ideal. Otra observación interesante es que si bien la diferencia
en la cantidad de pedidos entre el lote de 60 y el de 100 es de casi el doble,
la cantidad de rutas empleadas se encuentra en el orden de un 50% más. Como se
indicó anteriormente esto se debe a que gran parte de las rutas del lote de 60
pedidos partían utilizando vehículos cuya capacidad de transporte estaba lejos
de ser aprovechada al máximo y el ingreso de un mayor número de pedidos en el
lote de 100 permitió un mejor aprovechamiento del espacio de cada vehiculo. Por
otro lado en el lote de 350 pedidos se observa un aumento sustancial en la
cantidad de rutas empleadas y una diferencia marginal respecto a la cantidad
mínima de rutas que se podría haber utilizado en el caso ideal. Esto muestra
que para las condiciones de las pruebas realizadas, 100 pedidos resulta el
límite mínimo a partir del cual el desperdicio resultante en las rutas
generadas pasa a ser despreciable. Por lo que a medida que se agreguen más
pedidos, la cantidad de rutas utilizadas tenderá a parecerse cada vez más al
caso ideal planteado inicialmente. Esto tiene su explicación ya que al haber
tantos pedidos para elegir al armar una ruta, casi siempre es posible armar una
que vaya casi llena y por lo tanto se aprovechen mucho mejor los vehículos
utilizados.
Capítulo
7: Conclusiones
En base a los buenos resultados obtenidos
es claro que la herramienta implementada puede ser aplicada con éxito al
problema del ruteo de vehículos con ventanas de tiempo.
Una dificultad importante que surgió en el
desarrollo de la tesis fue la ausencia de lotes de prueba (datos de entrada)
cuyos resultados óptimos fueran conocidos, de modo de poder determinar la
performance del algoritmo en forma exacta. De todos modos basados en la cota
ideal presentada en el Capítulo 6 pudimos apreciar que los resultados obtenidos
por el algoritmo implementado para las instancias analizadas no se apartan
demasiado de esa cota.
La estrategia implementada demostró ser
capaz de obtener soluciones factibles y de buena calidad en muy cortos lapsos
de tiempo, lo cual es esencial dado el dinamismo del problema tratado y que el
tiempo entre la hora de ingreso y la hora de vencimiento de un pedido puede ser
muy breve.
A partir de las varias simulaciones
realizadas se logró obtener un conjunto de valores de referencia para los
parámetros del sistema (radio de acción, cantidad de diversificaciones,
cantidad de soluciones simultáneas, tamaño de la vecindad, etc.) que probaron
ser muy efectivos para tratar el problema en cuestión. Por lo tanto podrían
servir como punto de partida en caso de realizar la adaptación del sistema a
algún problema más particular.
En resumen se logró la implementación
exitosa de una heurística de búsqueda local basada en búsqueda Tabú que
mediante la elección de una vecindad adecuada permitió la exploración eficiente
de un espacio de soluciones de tamaño acotado que llevó a la obtención de
resultados muy satisfactorios.
La variedad en el tamaño de los lotes de
prueba y los tiempos medidos en la obtención de las soluciones muestra que el
algoritmo implementado facilitaría notablemente la tarea de un operador humano
de organizar la salida de vehículos según se especificó en el problema a
tratar.
Como conclusión final podemos apuntar que
la técnica de Búsqueda Tabú, implementada con las particularidades que se
presentaron en este trabajo, pueden aplicarse con éxito al problema dinámico de
ruteo de vehículos con ventanas de tiempo e indudablemente mejorarían el
rendimiento y eficiencia de este tipo de tareas en las distintas industrias.
Mejoras
y trabajo futuro
Entendemos que podrían realizarse diversas
mejoras al prototipo desarrollado, principalmente:
- La inclusión de un modelo matemático que ayude a comprender
mejor el problema.
- El desarrollo e implementación de nuevos métodos heurísticos que
aprovechen alguna particularidad del problema a tratar a fin de obtener
soluciones de mejor calidad.
- Incluir la generación de diversificaciones en las que se parta
de una solución inicial generada por un algoritmo goloso, para los casos
en los que se cuente con cierta masa crítica de pedidos en el inicio del sistema.
- El desarrollo de una interfaz gráfica de usuario que permita
interactuar en tiempo real con el prototipo. Esta interfaz debería brindar
como mínimo las siguientes funcionalidades:
- Ingreso de pedidos al sistema, con sus datos pertinentes.
- Selección de rutas a partir, permitiendo asignarlas a un
vehículo.
- Representación gráfica de un mapa de la zona de distribución y
trazado de las distintas rutas sobre el mapa.
- Notificación al usuario por parte del sistema de los momentos
en que se encuentran mejores soluciones para darle al usuario la opción
de tomar esa solución como nueva “solución actual”.
Bibliografía
[BH04] R. Bent y P.
Hentenryck. Scenario Based Planning for Partially Dynamic Vehicle Routing
Problems with Stochastic Customers. Operations Research, Vol. 52, No.
6, 2004.
[G86] F. Glover. Future
Paths for Integer Programming and Links to Artificial Intelligence. Computers
and Operations Research 5, 1986.
[G89] F. Glover. Tabu
Search – Part 1. ORSA Journal on Computing, vol. 1, no. 3, 1989.
[GJ79] Garey, M. and D.
Johnson, Computers and Intractability; A Guide to the Theory of
NP-Completeness, 1979
[GL93] F. Glover y M. Laguna. Tabu Search. Modern Heuristic Techniques for
Combinatorial Problems, Blackwell Scientific Publications, 1993.
[GLS96] M. Gendreau, G. Laporte, y R.
Seguin. A tabu
search heuristic for the vehicle routing problem with stochastic demands and
customers. Operations Research, 1996.
[HTW95] A. Hertz, E. Taillard y D. de Werra. A Tutorial On Tabu Search. Proc. of Giornate di Lavoro
AIRO'95 (Enterprise Systems: Management of Technological and Organizational
Changes), 1995.
[O76] I. Or. Traveling
Salesman-type Combinatorial Problems and Their Relation to the Logistics of
Regional Blood Banking. PhD thesis, Department of Industrial
Engineering and Management Sciences, Northwestern University, Evanston, IL.
[PKGR96] J. Y. Potvin, T. Kervahut, B. L. Garcia y J. M. Rousseau. The
Vehicle Routing Problem with Time Windows; Part I: Tabu Search. INFORMS
Journal on Computing 8, 1996.
[SOL] Marius M.
Solomon, VRPTW BENCHMARK PROBLEMS.
http://web.cba.neu.edu/~msolomon/problems.htm
[TV02] P. Toth, D.
Vigo, editors. The Vehicle Routing Problem. SIAM monographs on discrete
mathematics and applications, 2002
[TV03] P. Toth y D. Vigo. The Granular Tabu Search and its
Application to the Vehicle-Routing Problem. Informs Journal on Computing, Vol. 15, No. 4,
2003.
[VRPWEB] The VRP Web.
http://neo.lcc.uma.es/radi-aeb/WebVRP/